
《三角形全等的判定》全等三角形PPT(第3课时)
第一部分内容:生活情境
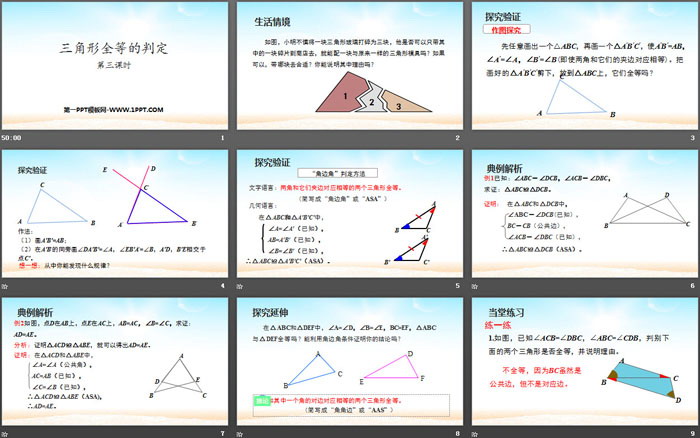
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?
... ... ...
三角形全等的判定PPT,第二部分内容:探究验证
作图探究
先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B(即使两角和它们的夹边对应相等)。把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B'=∠A,∠EB'A'=∠B,A'D,B'E相交于点C'。
“角边角”判定方法
文字语言:两角和它们夹边对应相等的两个三角形全等。
(简写成“角边角”或“ASA”)
几何语言:
在△ABC和△A′B′C′中,
∠A=∠A′(已知),
AB=A′B′(已知),
∠B=∠B′(已知),
∴△ABC≌△A′B′C′(ASA)。
... ... ...
三角形全等的判定PPT,第三部分内容:当堂练习
练一练
1.如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别下面的两个三角形是否全等,并说明理由。
不全等,因为BC虽然是公共边,但不是对应边。
2.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件,才能使△ABC≌△DEF(写出一个即可)。
3.已知:如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD。
证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°。
在△ABC和△ADC中,
∠1=∠2(已知),
∠B=∠D(已证),
AC=AC(公共边),
∴△ABC≌△ADC(AAS),
∴AB=AD。
... ... ...
三角形全等的判定PPT,第四部分内容:梳理反思
内容
两角及夹边对应相等的两个三角形全等。(简写成“ASA”)
两角和其中一个角的对边对应相等的两个三角形全等。(简写成“AAS”)
为证明线段和角相等提供了新的证法。
注意“角角边”、“角边角”中两角与边的区别。
关键词:人教版八年级上册数学PPT课件免费下载,三角形全等的判定PPT下载,全等三角形PPT下载,.PPT格式;











