



第十一单元 三角形,《多边形的内角和》PPT课件下载,共22页。
学习目标
1.理解多边形、正多边形以及多边形的内角、外角、对交线等概念。
2.会用不同的方法探索多边形的内角和,并能利用多边形内角和公式解决问题。
重点难点
重点:探索多边形的内角和。
难点:探索多边形内角和时,如何把多边形转化为三角形。
思考
连接四边形的任意对角线,将其分为两个三角形,而三角形的内角和为180°,那么任意四边形的内角和是360°吗?
证明:任意五边形的内角和等于540°
通过任意顶点连接对角线,将五边形分为三个三角形。
证明:任意五边形的内角和等于720°
通过任意顶点连接对角线,将六边形分为____个三角形。
课堂测试
例1:求八边形的内角和的度数。
例2:填空
(1)十二边形的内角和等于_____。
(2)已知一个多边形的内角和等于2340°,它的边数是_____ 。
(3)小明在计算多边形的内角和时求得的度数是1000°,他的答案正确吗?为什么?
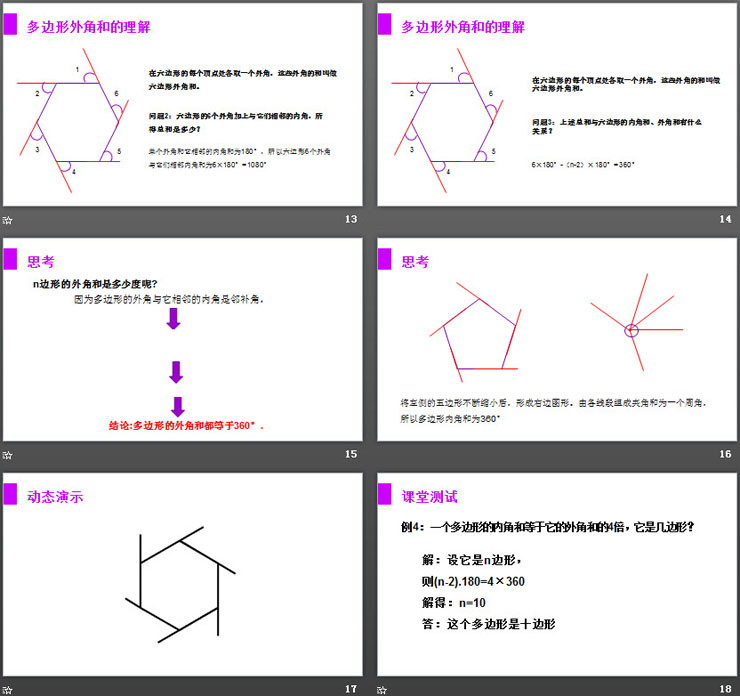
多边形外角和的理解
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形外角和。
问题1:任何一个外角同与它相邻的内角有什么关系?
问题2:六边形的6个外角加上与它们相邻的内角,所得总和是多少?
问题3:上述总和与六边形的内角和、外角和有什么关系?
关键词:多边形的内角和PPT课件免费下载,三角形PPT下载,.PPT格式;











