


《诱导公式二、三、四》三角函数PPT
第一部分内容:课标阐释
1.借助单位圆理解诱导公式的推导方法.
2.理解、掌握并熟记诱导公式二、三、四.
3.能够利用诱导公式解决三角函数的求值、化简与证明问题.
... ... ...
诱导公式二三四PPT,第二部分内容:自主预习
一、诱导公式二
1.观察单位圆,回答下列问题:
(1)角α与角π+α的终边有什么关系?
(2)角α与角π+α的终边与单位圆的交点P,P1有什么对称关系?
(3)在(2)中,点P,P1的坐标有什么关系?
提示:(1)在一条直线上,方向相反;(2)关于原点对称;(3)横、纵坐标都互为相反数.
2.填空
(1)角π+α与角α的终边关于原点对称(如图所示).
(2)诱导公式二:sin(π+α)=-sin α,cos(π+α)=-cos α,tan(π+α)=tan α.
3.做一做
(1)sin 225°=___________;
(2)tan4π/3=___________.
解析:(1)sin 225°=sin(180°+45°)=-sin 45°=-√2/2;
(2)tan4π/3=tan(π+π/3)=tanπ/3=√3.
答案:(1)-√2/2 (2)√3
二、诱导公式三
1.观察单位圆,回答下列问题:
(1)角α与角-α的终边有什么关系?
(2)角α与角-α的终边与单位圆的交点P,P1有什么对称关系?
(3)在(2)中,点P,P1的坐标有什么关系?
提示:(1)关于x轴对称;(2)关于x轴对称;(3)横坐标相等,纵坐标互为相反数.
2.填空
(1)角-α与角α的终边关于x轴对称(如图所示).
(2)诱导公式三:sin(-α)=-sin α,cos(-α)=cos α,tan(-α)=-tan α.
... ... ...
诱导公式二三四PPT,第三部分内容:探究学习
利用诱导公式解决求值问题
例1(1)求sin 585°cos 1 290°+cos(-30°)sin 210°+tan 135°的值;
(2)已知cos(α-55°)=-1/3,且α为第四象限角,求sin(α+125°)的值.
分析:(1)利用诱导公式将负角化为正角,进而化为锐角进行求值;(2)寻求α-55°与α+125°之间的关系,利用诱导公式进行化简.
解:(1)sin 585°cos 1 290°+cos(-30°)sin 210°+tan 135°
=sin(360°+225°)cos(3×360°+210°)+cos 30°sin 210°+tan(180°-45°)
=sin 225°cos 210°+cos 30°sin 210°-tan 45°
=sin(180°+45°)cos(180°+30°)+cos 30°·sin(180°+30°)-tan 45°
=sin 45°cos 30°-cos 30°sin 30°-tan 45°
=√2/2×√3/2-√3/2×1/2-1
=(√6 "-" √3 "-" 4)/4.
(2)因为cos(α-55°)=-1/3<0,且α是第四象限角,
所以α-55°是第三象限角.因此sin(α-55°)=-√(1"-" cos^2 "(" α"-" 55"°)" )=-(2√2)/3.又因为α+125°=180°+(α-55°),所以sin(α+125°)=sin[180°+(α-55°)]=-sin(α-55°)=(2√2)/3.
反思感悟 1.利用诱导公式解决给角求值问题的基本步骤:
2.利用诱导公式解决给值求值问题的策略:
(1)弄清楚已知条件与所求式中角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
... ... ...
诱导公式二三四PPT,第四部分内容:随堂演练
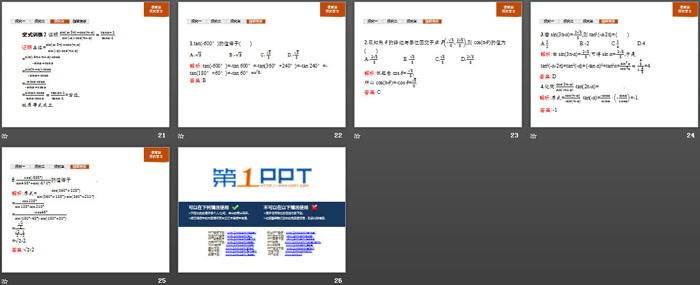
1.tan(-600°)的值等于( )
A.√3 B.-√3 C.√3/3 D.-√3/3
解析:tan(-600°)=-tan 600°=-tan(360°+240°)=-tan 240°=-tan(180°+60°)=-tan 60°=-
答案:B
2.已知角θ的终边与单位圆交于点P("-" √5/5 "," (2√5)/5),则cos(π-θ)的值为( )
A.-(2√5)/5 B.-√5/5 C.√5/5 D.(2√5)/5
解析:依题意cos θ=-√5/5,
所以cos(π-θ)=-cos θ=√5/5.
答案:C
... ... ...
关键词:高中人教A版数学必修一PPT课件免费下载,诱导公式二三四PPT下载,三角函数PPT下载,.PPT格式;











