




《不等式》等式与不等式PPT(第3课时不等式的解集第4课时一元二次不等式的解法)
第一部分内容:学 习 目 标
1.掌握不等式的解集及不等式组的解集.
2.解绝对值不等式.(重点、难点)
3.掌握一元二次不等式的解法.(重点)
4.能根据“三个二次”之间的关系解决简单问题.(难点)
核 心 素 养
1.通过数学抽象理解绝对值不等式.
2.通过一元二次不等式的学习,培养数学运算素养.
... ... ...
不等式PPT,第二部分内容:自主预习探新知
新知初探
1.不等式的解集与不等式组的解集
一般地,不等式的所有解组成的集合称为不等式的解集.对于由若干个不等式联立得到的不等式组来说,这些不等式的解集的____称为不等式组的解集.
2.绝对值不等式
一般地,含有____的不等式称为绝对值不等式.
3.数轴上两点之间的距离公式、中点坐标公式
一般地,如果实数a,b在数轴上对应的点分别为A,B,即A(a),B(b),则线段AB的长为AB=|a-b|,这就是数轴上两点之间的距离公式.数轴上线段AB的中点坐标公式为x=a+b2.
4.一元二次不等式的概念
一般地,形如ax2+bx+c>0的不等式称为一元二次不等式,其中a,b,c是常数,而且a≠0.
5.一元二次不等式的一般形式
(1)ax2+bx+c>0(a≠0).
(2)ax2+bx+c≥0(a≠0).
(3)ax2+bx+c<0(a≠0).
(4)ax2+bx+c≤0(a≠0).
思考2:不等式x2-y2>0是一元二次不等式吗?
提示:此不等式含有两个变量,根据一元二次不等式的定义,可知不是一元二次不等式.
6.一元二次不等式的解与解集
使一元二次不等式成立的未知数的值,叫做这个一元二次不等式的解,其解的集合,称为这个一元二次不等式的_____.
思考3:类比“方程x2=1的解集是{1,-1},解集中的每一个元素均可使等式成立”.不等式x2>1的解集及其含义是什么?
初试身手
1.不等式组2x+1>0,3x-2≤0的解集为( )
A.x-12≤x≤23 B.x12<x≤23
C.x-12<x<23 D.x-12<x≤23
2.不等式3x2-2x+1>0的解集为( )
A.x-1<x<13 B.x13<x<1
C.∅ D.R
3.不等式|x|-3<0的解集为________.
4.不等式-3x2+5x-4>0的解集为________.
... ... ...
不等式PPT,第三部分内容:合作探究提素养
求不等式组的解集
【例1】 不等式组12x-1≤0,x+3>0的解集是( )
A.x>-3 B.-3≤x<2
C.-3<x≤2 D.x≤2
C [12x-1≤0,①x+3>0,②
解不等式①得:x≤2,解不等式②得:x>-3,
∴不等式组的解集为-3<x≤2,故选C.]
规律方法
一元一次不等式组解集的求解策略
(1)一元一次不等式组的解集就是每个不等式解集的交集;
(2)求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).
解绝对值不等式
【例2】不等式|5-4x|>9的解集为________.
xx<-1或x>72 [∵|5-4x|>9,∴5-4x>9或5-4x<-9.
∴4x<-4或4x>14,
∴x<-1或x>72.
∴原不等式的解集为xx<-1或x>72.]
规律方法
1.|x|<a与|x|>a型不等式的解法
不等式 a>0 a=0 a<0
|x|<a {x|-a<x<a} ∅ ∅
|x|>a {x|x>a或x<-a} {x|x∈R且x≠0} R
2.|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法
(1)|ax+b|≤c⇔-c≤ax+b≤c;
(2)|ax+b|≥c⇔ax+b≥c或ax+b≤-c.
一元二次不等式的解法
【例3】解下列不等式:
(1)2x2+7x+3>0;
(2)-4x2+18x-814≥0;
(3)-2x2+3x-2<0.
规律方法
解不含参数的一元二次不等式的一般步骤
1化标准.通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
2判别式.对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
3求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
4画草图.根据一元二次方程根的情况画出对应的二次函数的草图.
5写解集.根据图像写出不等式的解集.
课堂小结
1.不等式(组)的解集要写成集合形式,不等式组的解集是每个不等式解集的交集.
2.解绝对值不等式的关键就是去掉绝对值,利用绝对值不等式的几何意义求解,体现了数形结合的思想.
3.解一元二次不等式的常见方法
(1)图像法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图像的简图;
③由图像得出不等式的解集.
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m<n时,若(x-m)(x-n)>0,则可得{x|x>n或x<m};
若(x-m)(x-n)<0,则可得{x|m<x<n}.
有口诀如下:大于取两边,小于取中间.
4.含参数的一元二次型的不等式
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”,讨论需从如下三个方面进行考虑:
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:两根(Δ>0),一根(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,x1=x2,x1<x2.
5.由一元二次不等式的解集可以逆推二次函数的开口及与x轴的交点坐标.
... ... ...
不等式PPT,第四部分内容:当堂达标固双基
1.思考辨析
(1)mx2-5x<0是一元二次不等式.( )
(2)若a>0,则一元二次不等式ax2+1>0无解.( )
(3)若一元二次方程ax2+bx+c=0的两根为x1,x2(x1<x2),则一元二次不等式ax2+bx+c<0的解集为{x|x1<x<x2}.( )
(4)若|x|>c的解集为R,则c≤0.( )
[提示](1)错误.当m=0时,是一元一次不等式;当m≠0时,是一元二次不等式.
(2)错误.因为a>0,所以不等式ax2+1>0恒成立,即原不等式的解集为R.
(3)错误.当a>0时,ax2+bx+c<0的解集为{x|x1<x<x2},否则不成立.
(4)显然c=0不成立,错误.
2.已知数轴上A(3),B(-5),则线段AB中点M的坐标为________.
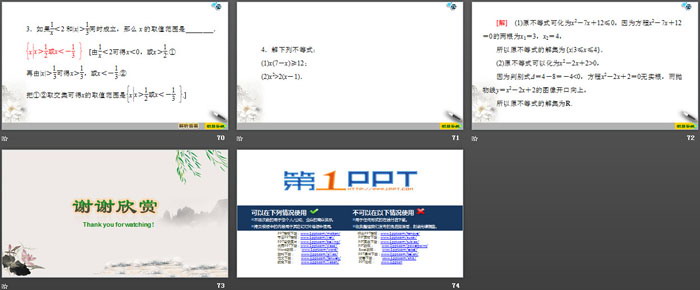
3.如果1x<2和|x|>13同时成立,那么x的取值范围是________.
4.解下列不等式:
(1)x(7-x)≥12;
(2)x2>2(x-1).
... ... ...
关键词:高中人教B版数学必修一PPT课件免费下载,不等式PPT下载,等式与不等式PPT下载,不等式的解集PPT下载,一元二次不等式的解法PPT下载,.PPT格式;











