



《锐角三角函数》直角三角形的边角关系PPT课件(第1课时),共28页。
学习目标
理解锐角三角函数正切的意义,会求直角三角形中的锐角正切值.
经历探索直角三角形中边角关系的过程,发展学生数形结合的能力;通过有关正切值的计算,发展学生的计算能力.
通过小组合作活动,培养学生的合作意识;通过解决实际问题,让学生体会数学与生活的密切联系.
... ... ...
情境导入
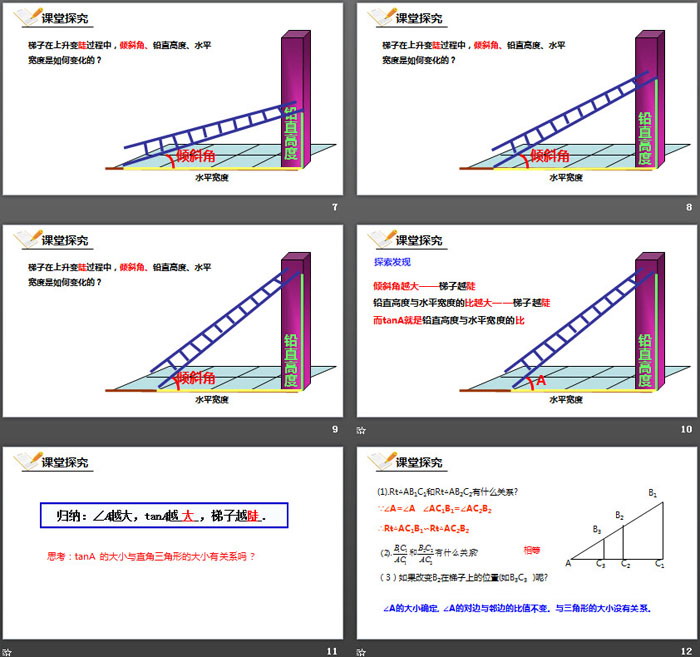
哪个梯子更陡?你是怎样判断的?有几种方法?
想一想
赵明想通过测量B1C1及AC1,算出它们的比来说明梯子的倾斜程度却因身高原因不能直接测量梯子顶端到墙脚的距离B1C1 ,而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.
你同意小亮的看法吗?
... ... ...
课堂探究
梯子在上升变陡过程中,倾斜角、铅直高度、水平宽度是如何变化的?
探索发现
倾斜角越大——梯子越陡
铅直高度与水平宽度的比越大——梯子越陡
而tanA就是铅直高度与水平宽度的比
... ... ...
要点归纳
判断梯子是否更陡,有如下方法:
1.可以利用倾斜角的大小比较,倾斜角越大,梯子越陡.
2.可以利用倾斜角的对边与邻边的比值大小来判断,比值越大,梯越陡.
当倾斜角确定时,它的对边与邻边的比值也随之确定的,即:这个比值只与倾斜角的大小有关,而与直角三角形的大小无关.
... ... ...
新知讲解
正切也经常用来描述山坡的坡度.坡面与水平面的夹角称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切.
例如,有一山坡在水平方向上每前进100m就升高60m,求该山坡的坡度i
应用中应该注意的几个问题:
1.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
2.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位)
3.tanA是在直角三角形中定义的,∠A是一个锐角(注意构造直角三角形)。
4.tanA的大小只与∠A的大小有关,而与直角三角形的大小无关。
... ... ...
谈收获
一、梯子倾斜度及判断
1.可以利用倾斜角的大小比较,倾斜角越大,梯子越陡.
2.可以利用倾斜角的对边与邻边的比值大小来判断,比值越大,梯子越陡.
二、正切
∠A的正切:∠A的对边与邻边的比值.
∠A越大,tanA越大 ,梯子越陡.
... ... ...
个性化作业
1.如图,△ABC是等腰三角形,你能根据图中所 给数据求出tanC吗?
2.如图,某人从山脚下的点A走了200m后到达山顶的点B,已知点B到山脚的垂直距离为55m,求山的坡度(结果精确到0.001).
关键词:北师大版九年级下册数学PPT课件免费下载,锐角三角函数PPT下载,直角三角形的边角关系PPT下载,.PPT格式;











