


《指数函数》指数函数与对数函数PPT
第一部分内容:课标阐释
1.理解指数函数的概念和意义,能画出具体指数函数的图象.
2.初步掌握指数函数的性质,并能解决与指数函数有关的定义域、值域、定点问题.
3.逐步体会指数函数在实际问题中的应用.
... ... ...
指数函数PPT,第二部分内容:自主预习
一、指数函数的定义
1.细胞分裂时,由一个分裂成两个,两个分裂成四个……设1个细胞分裂x次后得到的细胞个数为y.
(1)变量x与y间存在怎样的关系?
提示:y=2x,x∈N*.
(2)上述对应关系是函数关系吗?为什么?
提示:是.符合函数的定义.
2.如果x∈R,等式y=2x还表示y是x的函数吗?如果是,其解析式有何结构特征?
提示:是.结构特征:等式右边是指数形式,底数为常数,指数是变量.
3.填空:
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中指数x是自变量, 定义域是R.
4.指数函数定义中为什么规定了a>0且a≠1?
提示:将a如数轴所示分为:a<0,a=0,0<a<1,a=1和a>1五部分进行讨论:
(1)如果a<0,如y=(-4)x,这时对于x=1/4,x=1/2等,在实数范围内函数值不存在;
(2)如果a=0,{■("当" x>0"时," a^x "恒等于" 0"," @"当" x≤0"时," a^x "无意义;" )┤
(3)如果a=1,y=1x=1,是个常数函数,没有研究的必要;
(4)如果0<a<1或a>1,即a>0且a≠1,x可以是任意实数.
5.做一做
若函数y=(a-2)ax是指数函数,则( )
A.a=1或a=3 B.a=1
C.a=3 D.a>0且a≠1
解析:若函数y=(a-2)ax是指数函数,
则{■(a"-" 2=1"," @a>0"且" a≠1"," )┤解得a=3.
答案:C
二、指数函数y=ax(a>0,且a≠1)的图象与性质
分别在同一平面直角坐标系内画出y=2x与y=(1/2)^x的图象及y=3x与y=(1/3)^x的图象,通过观察具体的指数函数的图象,归纳、抽象出y=ax(a>0,且a≠1)的图象与性质.
(1)图象分布在哪几个象限?这说明了什么?
提示:图象分布在第一、二象限,说明值域为(0,+∞).
(2)猜想图象的上升、下降与底数a有怎样的关系?对应的函数的单调性如何?
提示:它们的图象都在x轴上方,向上无限伸展,向下无限接近于x轴;当底数a大于1时图象上升,为增函数;当底数a大于0小于1时图象下降,为减函数.
(3)图象是否经过定点?这与底数的大小有关系吗?
提示:图象恒过定点(0,1),与a无关.
... ... ...
指数函数PPT,第三部分内容:探究学习
指数函数的概念
例1 (1) 如果指数函数y=f(x)的图象经过点("-" 2"," 1/4),那么f(4)f(2)等于____________.
(2)已知函数y=(a2-3a+3)ax是指数函数,求a的值.
分析:(1)设出指数函数f(x)的解析式,然后代入已知点的坐标求解参数,从而确定函数解析式,最后代值求解;(2)依据指数函数的形式定义,确定参数a所满足的条件求解.
(1)解析:设f(x)=ax(a>0,a≠1),
∴a-2= .∴a=2.∴f(4)f(2)=24·22=64.
答案:64
(2)解:由y=(a2-3a+3)ax是指数函数,可得{■(a^2 "-" 3a+3=1"," @a>0",且" a≠1"," )┤
解得{■(a=1"或" a=2"," @a>0",且" a≠1"," )┤故a=2.
反思感悟指数函数是一个形式定义,其特征如下:
变式训练(1)已知指数函数的图象经过点P(-1,3),则f(3)=_________.
(2)已知函数f(x)=(a2-2a+2)(a+1)x为指数函数,则a=_________.
解析:(1)设指数函数为f(x)=ax(a>0且a≠1),由题意得a-1=3,
解得a=1/3,所以f(x)=(1/3)^x,故f(3)=(1/3)^3=1/27.
(2)函数f(x)=(a2-2a+2)(a+1)x是指数函数,
∴{■(a^2 "-" 2a+2=1"," @a+1>0"," @a+1≠1"," )┤解得a=1.
答案:(1)1/27 (2)1
指数函数的图象问题
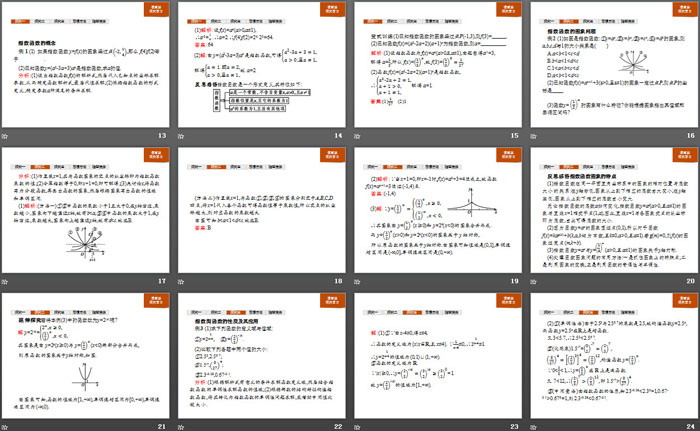
例2 (1)如图是指数函数:①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.a<b<1<c<d
B.b<a<1<d<c
C.1<a<b<c<d
D.a<b<1<d<c
(2)已知函数f(x)=ax+1+3(a>0,且a≠1)的图象一定过点P,则点P的坐标是____.
(3)函数y=(1/2)^("|" x"|" )的图象有什么特征?你能根据图象指出其值域和单调区间吗?
... ... ...
指数函数PPT,第四部分内容:思想方法
换元法在求函数值域中的应用
典例 已知函数y=(1/4)^x-(1/2)^x+1的定义域为[-3,2].
(1)求函数的单调区间;
(2)求函数的值域.
分析:原函数可以看作是y关于(1/2)^x的二次函数,换元后转化为二次函数在闭区间上的最值问题.
反思感悟 1.定义域、值域的求解思路
形如y=af(x)的函数的定义域就是f(x)的定义域.
求形如y=af(x)的函数的值域,应先求出u=f(x)的值域,再结合y=au的单调性求出y=af(x)的值域.若a的取值范围不确定,则需对a进行分类讨论.
形如y=f(ax)的函数的值域,要先求出u=ax的值域,再结合y=f(u)的单调性确定出y=f(ax)的值域.
2.求解技巧
复合函数的值域,往往用换元法解决,但要注意新元和旧元的关系.
... ... ...
指数函数PPT,第五部分内容:随堂演练
1.函数y=2-x的大致图象是 ( )
解析:y=2-x=(1/2)^x.
答案:B
2.已知集合M={y∈R|y=2x,x>0},N={x∈R|x2-2x<0},则M∩N=( )
A.(1,2) B.(1,+∞)
C.[2,+∞) D.(-∞,0]∪(1,+∞)
答案:A
3.已知2x>21-x,则x的取值范围是( )
A.R B.x<1/2
C.x>1/2 D.⌀
解析:∵2x>21-x,∴x>1-x,即x>1/2.
答案:C
... ... ...
关键词:高中人教A版数学必修一PPT课件免费下载,指数函数PPT下载,指数函数与对数函数PPT下载,.PPT格式;











