




《点和圆的位置关系》圆PPT下载
第一部分内容:探究
问题1:观察,图中点A,点B,点C与圆的位置关系分别是什么?
问题2:设⊙O 半径为r,说出来点A,点B,点C 与圆心O 的距离与半径的关系.
问题3:反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
归纳
设⊙O 半径为r,点P 到圆心的距离OP =d,则有:
这个符号读作“等价于”,它表示从该符号的左端可以推出右端,右端也能推出左端.
你知道击中靶上不同位置的成绩是如何计算的吗 ?
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域.
这些区域用由高到底的环数来表示,射击成绩 用弹着点位置对应的环数来表示.
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
... ... ...
点和圆的位置关系PPT,第二部分内容:例题
已知⊙O 的半径为10cm,A,B,C 三点到圆心O 的距离分别为8cm,10cm,12cm,则点A,B,C 与⊙O 的位置关系是:
点A在_________.
点B在_________.
点C在_________.
如图所示,已知⊙O 和直线l,过圆心O 作OP⊥l,P 为垂足,A,B,C为直线l上三个点,且PA=2cm,PB =3cm,PC =4cm,若⊙O的半径为5cm,OP=4cm,判断A,B,C三点与⊙O的位置关系.
点A在_________.
点B在_________.
点C在_________.
... ... ...
点和圆的位置关系PPT,第三部分内容:补充题
⊙O 的半径为 5 cm,O 到直线l的距离OP=3cm,Q 为l上一点且PQ =4.2cm,点Q 在⊙O _________.
如图, 数轴上半径为1的⊙O 从原点O 开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P 以每秒2个单位的速度向左运动,经过_________秒后,点P在⊙O 上.
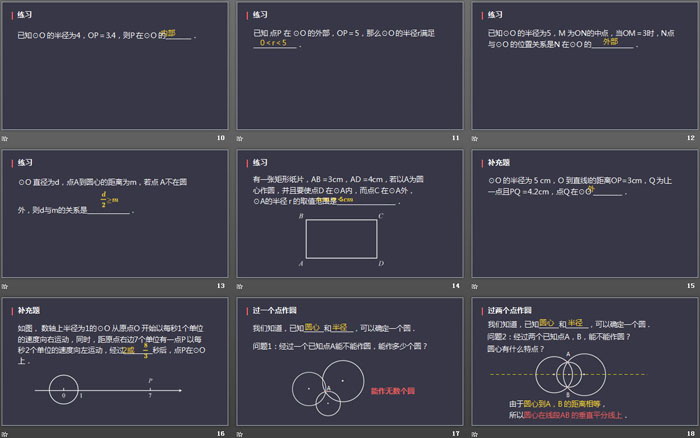
过一个点作圆
我们知道,已知______和_______,可以确定一个圆.
问题1:经过一个已知点A能不能作圆,能作多少个圆?
过两个点作圆
总结:过已知点作圆,关键就是确定______.
问题3:经过不在同一直线上的三个点A,B,C 能不能作圆?如果能,怎么确定圆心?
圆心O到A,B,C 的距离都相等
所以O 既在线段AB 的垂直平分线上
又在线段BC 的垂直平分线上
垂直平分线的交点就是圆心O
以O为圆心,OA( 或OB,OC )为半径作圆即为所求.
过三个点作圆
问题4:经过不在同一直线上的三个点A,B,C 能作几个圆?
由于圆心O是唯一确定的,
所以圆也是唯一确定的.
不在同一条直线上 的三个点确定一个圆.
... ... ...
点和圆的位置关系PPT,第四部分内容:平行线性质定理的证明
用反证法证明平行线的性质“两直线平行,同位角相等”.
已知AB∥CD,求证:∠1=∠2.
假设∠1≠∠2,过点O 作A’B’,
使∠EOB’=∠2.
根据“同位角相等,两直线平行”,
可得A’B’∥CD.
由此可知,过点O 的直线AB和直线A’B’都与直线CD平行.
讨论一下,你们能发现矛盾之处吗?
... ... ...
点和圆的位置关系PPT,第五部分内容:总结
这节课我们学会了什么?
点和圆的位置关系:
设⊙O半径为r,点P到圆心的距离OP=d,则有:
不共线的三点确定一个圆:
不在同一条直线上 的三个点确定一个圆.
三角形的外接圆:
过任意三角形的三个顶点都可以作一个唯一确定的圆.
这个圆心叫三角形的外心,
是三角形三边垂直平分线的交点.
反证法:
不是直接从命题的已知得结论,而是假设命题的结论不成立
由此经过推理的出矛盾,由矛盾判定假设不正确,
从而得到原命题成立,
这种方法叫做反证法.
关键词:人教版九年级上册数学PPT课件免费下载,点和圆的位置关系PPT下载,圆PPT下载,.PPT格式;











